课题组成员:高以天,于鑫
本课题组主要致力于流体和等离子体等领域中的非线性波动力学的解析和数值研究,研究内容包括孤子解和畸形波解的构造、波动的传播和相互作用特点及不均匀性对波动的影响等。在解析研究方面扩展了双线性方法、达布变换方法等的应用范围,求得了一系列新解;在数值方面利用差分方法、谱方法及有限元软件研究了水波及微流动的特点;在波动分析方面基于特征线方法等研究了弹性、非弹性相互作用,以及物理参数与波动特点的关系。课题组自2009年以来在PHYSICALREVIEWE、ANNALS OFPHYSICS、EPL等期刊共发表SCI论文50余篇,SCI他引200余次。
1)在浅水波类模型研究方面,将孤子传播过程中的表现形式分为速度、振幅、背景、宽度几部分,利用特征线方法和图像分析,揭示了这些特征与色散系数、耗散系数、阻尼系数和外力项的关系,得出了孤子的整个传播过程是各个变系数效应综合作用的结论;分析了波数变化对孤子相互作用模式、特殊孤子结构的影响规律;利用渐近分析解释了一种波形不随参数发生改变的特殊掩盖情况;讨论了在变系数和波数耦合作用情况下的拟弹性相互作用、拟孤子融合、拟孤子分裂等现象;研究了非自治孤子解析解和波前解,揭示了非线性波的传播特性和相互作用规律;利用Bell多项式和辅助变量构造了一些模型的双线性形式,并利用双线性方法构造了多孤子解。
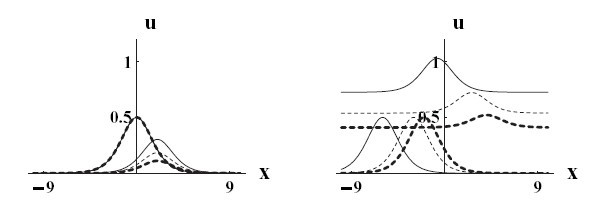
孤波速度、振幅、背景与阻尼系数的相互关系
2)在深水波类模型研究方面,基于耦合非线性Schrodinger系统对束缚态矢量孤子进行了分类,并分析了其与单孤子相互作用中的形变和能量重新分配的规律;研究了束缚态矢量孤子在随机环境中的动力学问题,发现在均匀随机扰动下,束缚态矢量孤子会历经扭曲和破裂两个普遍过程,同时当不对称的扰动加载在两个模态中时,孤子会发生对称性恢复的现象,对于不均匀随机扰动,束缚态矢量孤子会在一定的传播距离中在两个模态中发生孤子交换的现象,此现象与扰动的强度和孤子的初始粘连度紧密相关;利用三耦合Gross-Pitaevskii方程研究了随时间变化调制的非自治物质波,通过调节外势、原子增益/损耗及耦合系数,得到了几种非自治物质波孤子和畸形波,研究发现外势、原子增益/损耗能影响物质波孤子的传播和束缚孤子的持续时间和频率,但是对正面的相互作用孤子影响很少,通过数值模拟,实现了在5%初始随机噪声扰动下物质波孤子的稳定发展,原子的相互作用受到随时间变化调制的影响;利用广义达布变换构造了几类Schrodinger类系统的高阶畸形波解,研究了波的传播和相互作用,发现频率影响波谷的数目、畸形波的类型和传播方向,影响高阶畸形波相互作用的类型,研究了二阶、三阶畸形波正面相互作用。
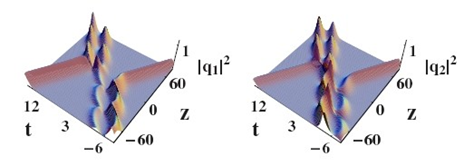
相互作用中的形变









